XBeam2D Analysis: Difference between revisions
(Created page with "=== Deflection calculation timber Eurocode === The deflection calculation according to the Eurocode has several parts: * '''w-on:''' Elastic deflection according with the standard elastic modulus of the timber type due to the dead load. * '''w-creep''': Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with normal elastic modulus. 2. Deflection due to combination 6.16b with elastic modulus is Emean/(1+kdef). w-creep=2-1. * '''w-k:''' Deflection du...") |
No edit summary |
||
| Line 2: | Line 2: | ||
The deflection calculation according to the Eurocode has several parts: | The deflection calculation according to the Eurocode has several parts: | ||
* '''w- | * '''w-inst :''' Elastic deflection according with the standard elastic modulus of the timber type due to the dead load. | ||
* '''w-creep''': Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with normal elastic modulus. 2. Deflection due to combination 6.16b with elastic modulus is Emean/(1+kdef). w-creep=2-1. | * '''w-creep''': Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with normal elastic modulus. 2. Deflection due to combination 6.16b with elastic modulus is Emean/(1+kdef). w-creep=2-1. | ||
* '''w-k:''' Deflection due to the 6.14 combination(SLS). | * '''w-k:''' Deflection due to the 6.14 combination(SLS). | ||
* '''w-fin''': | * '''w-fin''': w-k + w-creep | ||
* '''w-add''': | * '''w-add''': w-k + w-creep - w-inst | ||
=== Deflection calculation concrete Eurocode === | === Deflection calculation concrete Eurocode === | ||
The | The physic non-linear properties are used in the calculation using the M-kappa diagram. The stiffness differs per point in the beam due to reinforcement/cracked/non-cracked. | ||
The beam is separated into parts. For each part the non-linear properties are calculated based on the reinforcement and M-kappa diagram. Separate calculation are made for the ULS and SLS. | |||
[[File:XBeam2DCalculationDeflectionConcrete1.png|629x629px]] | [[File:XBeam2DCalculationDeflectionConcrete1.png|629x629px]] | ||
| Line 25: | Line 20: | ||
w- | '''w-inst :''' Elastic deflection according with the standard elastic modulus of the timber type due to the dead load.(short term EI) | ||
'''w-creep''': Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with short term EI. 2. Deflection due to combination 6.16b with elastic modulus is long term EI. w-creep = w;qp;long - w;qp;short. | |||
w-k | '''w-k:''' Deflection due to the 6.14 combination(SLS). | ||
w- | '''w-fin''': w-k + w-creep | ||
w- | '''w-add''': w-k + w-creep - w-inst | ||
Revision as of 04:43, 6 September 2022
Deflection calculation timber Eurocode
The deflection calculation according to the Eurocode has several parts:
- w-inst : Elastic deflection according with the standard elastic modulus of the timber type due to the dead load.
- w-creep: Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with normal elastic modulus. 2. Deflection due to combination 6.16b with elastic modulus is Emean/(1+kdef). w-creep=2-1.
- w-k: Deflection due to the 6.14 combination(SLS).
- w-fin: w-k + w-creep
- w-add: w-k + w-creep - w-inst
Deflection calculation concrete Eurocode
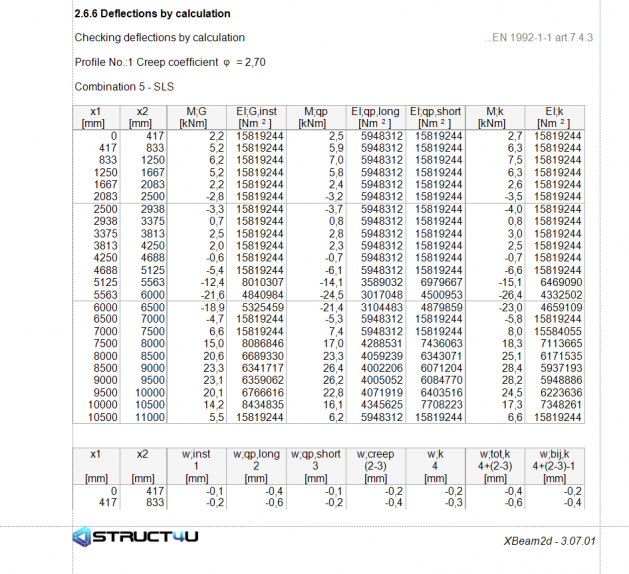
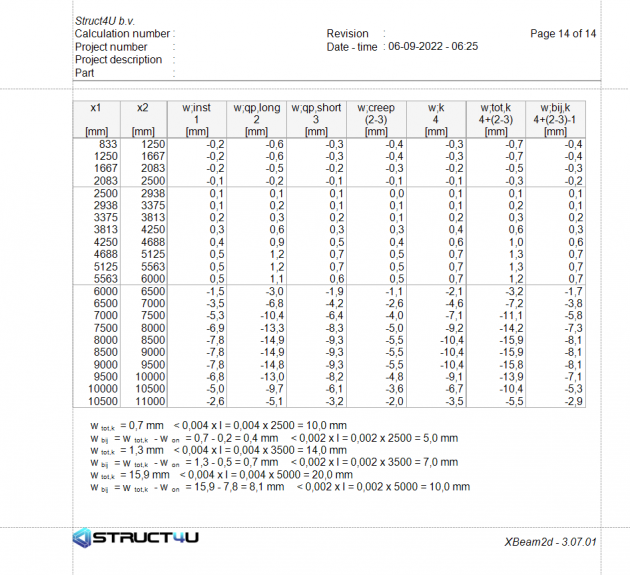
The physic non-linear properties are used in the calculation using the M-kappa diagram. The stiffness differs per point in the beam due to reinforcement/cracked/non-cracked.
The beam is separated into parts. For each part the non-linear properties are calculated based on the reinforcement and M-kappa diagram. Separate calculation are made for the ULS and SLS.
w-inst : Elastic deflection according with the standard elastic modulus of the timber type due to the dead load.(short term EI)
w-creep: Deflection due to creep. 1. Deflection due to load combination SLS 6.16b with short term EI. 2. Deflection due to combination 6.16b with elastic modulus is long term EI. w-creep = w;qp;long - w;qp;short.
w-k: Deflection due to the 6.14 combination(SLS).
w-fin: w-k + w-creep
w-add: w-k + w-creep - w-inst