Documentation ANSI

BACK

XFEM4U has a fully integrated ANSI/AISC 360-16 steel design module. Steel test / design rules according to the newest / latest American standards. You are up-to-date with the latest standards.

In XFEM4U all design checks are based on Direct Analysis Method of Design  according to AISC 360-16 Section C1.1 using Design for Strength Using Load and Resistance Factor Design (LRFD).

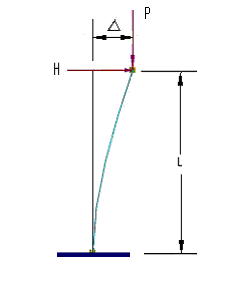
The direct analysis method of design used, is based on elastic P-Δ-only second-order analysis. Imperfections (initial system imperfections) will be automatically included in calculating load combination(s).

This is a very accurate calculation method and is applicable for every type of frame. Sway or braced/non-sway frames. Also, there is no need to calculate (error-prone) buckling lengths (effective lengths) anymore. The geometrical non-linear analysis (Second-order analysis) ensures global buckling stability check.

The way steel check according to the  ANSI/AISC 360-16 is implemented

Explanation:

• P-Delta (P-Δ) is taken into account in the elastic second-order analysis.
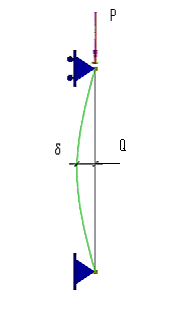
• P-delta (P-δ) - second order effect associated with the member curvature - is not taken into account.

According to AISC 360-16 Section C2.1 (b):

Because the analysis is a P-Δ-only second-order analysis, the requirement for considering P-δ effects in the evaluation of individual members can be satisfied by applying the B1 multiplier defined in Appendix 8 to the required flexural strength of the member. All bending moments in each member subject to compression and flexure, are multiplied with B1 automatically, according to formula (A-8-1) and (A-8-3) in Appendix 8.2.

This means that the individual stability of the members must be checked according to chapter E, whereby the buckling length (effective length) may be set equal to the unbraced length (K=1,00) according to AISC 360-16 Section C3 CALCULATION OF AVAILABLE STRENGTHS. By applying a geometric non-linear analysis, the moments and forces are of course including all second-order effects.

In XFEM4U, the global initial sway imperfections (or initial system imperfections) are taken into account automatically, by direct modeling of these imperfections in the analysis as specified in AISC 360-16 Section C2. 2a Direct Modeling of Imperfections. The default out-of-plumbness ratio is 1/500.

This approach has many advantages:

• There is no need to calculate (error-prone) buckling lengths (effective lengths) any more. Buckling lengths are not calculated correctly in all cases and are certainly not load independent.
• There is no need to make a choice for the type of framework, sway or non-sway. When the framework is sensitive to 2nd order, it follows directly from the analysis.
• By global initial sway imperfections of the framework, the calculation process (the iteration) also works well with a symmetrical construction and symmetrical load.
• Adjacent loads can easily be taken into account.
• Lateral stability is also included in the stability check according to chapter H.

P-Delta (P-Δ)   

                                                 

P-delta (P-δ)