|
|
| Line 1: |
Line 1: |
|
| |
| ==Buckling==
| |
|
| |
| '''XFEM4U''' has a fully integrated Eurocode EN 1993 steel design module. Steel test / design rules according to the newest / latest European standards. You are up-to-date with the latest standards. In '''XFEM4U''' all Eurocode design checks are based on a geometrically non-linear analysis. Imperfections (initial sway imperfections) will be automatically included in calculating load combination(s).
| |
|
| |
|
| |
|
| |
| This is a very accurate calculation method and is applicable for every type of frame. Sway or braced/non-sway frames. Also, there is no need to calculate (error-prone) buckling lengths anymore. The geometrical non-linear analysis (Second-order analysis) ensures global buckling stability check.
| |
|
| |
|
| |
| '''The way steel check according to the Eurocode is implemented'''
| |
|
| |
|
| |
| '''Explanation:'''
| |
|
| |
| According to Eurocode EN 1993-1-1 art. 5.2.2 (7) a) no individual stability check for the members according to 6.3 is necessary if second order effects in individual members and relevant member imperfections (see 5.3.4) are totally accounted for in the global analysis of the structure. (Global initial sway imperfections and relatively initial local bow imperfections of members for flexural buckling).
| |
|
| |
|
| |
| In '''XFEM4U''', the global initial sway imperfections according to art. 5.3.2 (3) a) are taken into account automatically. However, the relatively initial local bow imperfections of members for flexural buckling according to art. 5.3.2 (3) b) are not.
| |
|
| |
|
| |
| This means that the individual stability of the elements must be checked according to 6.3, whereby the buckling length may be set equal to the system length. According to art. 5.2.2 (7) b). By applying a geometric non-linear analysis, the moments and forces are of course including all second-order effects.
| |
|
| |
|
| |
| This approach has many advantages:
| |
|
| |
| *There is no need to calculate (error-prone) buckling lengths anymore. Buckling lengths are not calculated correctly in all cases and are certainly not load independent.
| |
| *There is no need to make a choice for the type of framework, sway or non-sway. When the framework is sensitive to 2nd order, it follows directly from the analysis.
| |
| *By global initial sway imperfections of the framework, the calculation process (the iteration) also works well with a symmetrical construction and symmetrical load.
| |
| *Adjacent loads can easily be taken into account.
| |
| *Lateral stability is also included in the stability check according to 6.3.3.
| |
|
| |
| ==Tapered beam== | | ==Tapered beam== |
|
| |
|
Revision as of 06:49, 17 September 2022
Tapered beam
You can optionally enter a tapered beam. The tab "Profile end" is activated. Here you can enter the 2nd profile at the end of the bar. Attention! The basic shape of the profile (H-, U-, L-shape, etc.) must match that of the profile at the beginning of the beam.
Force distribution
For the mechanics calculation, the beam is automatically divided into a number of beam parts with a length corresponding to the average profile height. The profile section properties such as moment of inertia are calculated in the middle of each beam part. A constant moment of inertia is calculated for each beam part. Because the beam parts are quite short, this approach proves to be sufficiently accurate.
Stress testing
For stress testing, the profile section properties are calculated per section (per x-distance). Thus, this calculation is exact.
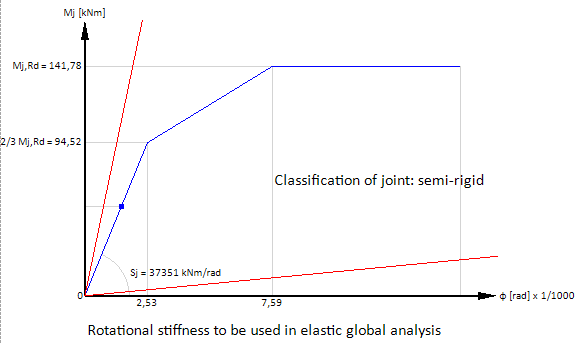
Calculation Steel Joints rigidity
Load-dependent rotational rigidity
In XFEM4U a geometric nonlinear analysis (GNL) is calculated by standard. The force distribution is determined iteratively. The beam-column moment connections can be entered. The rotational stiffness of all connections per iteration step is determined. Based on the occurring moment in the beam connection, the rotational rigidity diagram of the designed connection (see diagram below) determines a rotational stiffness or spring stiffness which is then used in the next iteration step. The iteration stops when there are no more changes in the force distribution.
In XFEM4U, a load-dependent rotational rigidity is therefore taken into account for all moment connections. This gives the most accurate result and leads to an economically optimal design.
At small moments (under 2/3 Mj, Rd), initial rotational stiffness Sj, ini is calculated. At larger moments with the rotational stiffness Sj corresponding to the bending moment Mj, Ed, the trilinear rotational rigidity diagram is used. See the diagram below.